什麼是萬有引力定律？概念、公式、陳述、公式使用範例

我們解釋了萬有引力定律是什麼，它的公式和陳述是怎樣的。此外，還提供了其公式的使用範例。

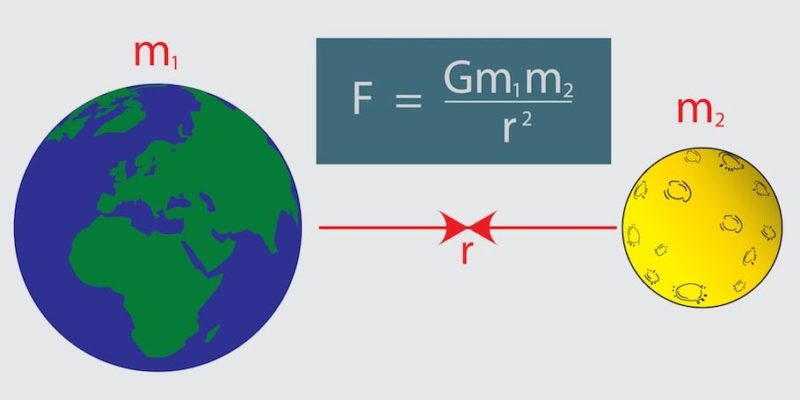
萬有引力定律描述了物體之間的引力相互作用。

什麼是萬有引力定律？

萬有引力定律是其中一條定律 物理的 以撒牛頓 （Isaac Newton） 在 1687 年的《自然哲學原理》一書中提出。它描述了大品質天體之間的引力相互作用，並建立了引力使用品質的身體。

為了制定這個定律，牛頓推匯出兩個品質相互吸引的力與它們的品質除以將它們平方的距離的乘積成正比。這些推論是通過觀察.

該定律意味著兩個天體越接近、品質越大，它們之間的吸引力就越強烈。與其他牛頓定律一樣，它代表了科學知識的時代。

然而，今天我們知道，在達到一定質量之後，該定律就失去了有效性（在超大品質物體的情況下），有必要使用阿爾伯特·愛因斯坦在 1915 年制定的廣義相對論定律。因此，萬有引力定律是愛因斯坦定律的近似值，但它對於理解大多數萬有引力現象仍然有用。太陽系.

• 另請參閱：重力場

萬有引力定律的陳述

該牛頓定律的正式聲明認為：

“兩個物體相互吸引的力與它們的品質乘積成正比，與它們之間的距離的平方成反比。”

這意味著任何兩個物體都以或大或小的力相互吸引，這取決於它們的品質是大是小，以及它們之間的距離。

萬有引力定律的公式

萬有引力定律的基本公式如下：

F = |（G . m₁.m₂） / r^² | .r^*

哪裡：

• F 是兩個品質之間的吸引力

• G 是萬有引力常數 （ 6.673484.10^-11牛米²/公斤²)

• m₁是其中一個物體的品質

• m₂它是另一個物體的品質

• 將它們分開的距離。

• r^* 是指示力方向的單位向量。

如果計算每個物體的吸引力（品質 1 對品質 2 產生的力，反之亦然），我們將有兩個模量相等且方向相反的力。要獲得符號的這種差異，有必要將方程寫成如下：

F₁₂= |G .m₁.m₂/ （R1₁-r₂)³| .（r₁-r₂)

其中 1 x 2 變化，我們得到每種情況的強度。以這種方式寫成，這向量（r₁-r₂） 給出每個力的正確方向（符號）.

萬有引力定律的例子

讓我們解決幾個練習作為此公式應用的範例。

• 假設一個品質為 800 kg 的品質和另一個品質為 500 kg 的品質在真空中被吸引，相隔 3 米的空間。我們如何計算他們所體驗到的吸引力？
  
  只需應用公式：
  F = G. （m₁.m₂）/r²
  
  將是什麼： F = （6.67×10^-11牛米²/公斤²) .（800 公斤 . 500 公斤） / （3 米）²
  
  然後：F = 2.964 x 10^-6N.

• 另一個練習：我們應該將兩個品質為 1 kg 的物體相距多遠，以便它們以 1 N 的力相互吸引？
  
  從相同的公式開始：
  F = G. （m¹.m²）/r²
  
  我們會拉開距離，保持這種距離r²= 克（m₁.m₂）/ F
  換句話說，r = √（G.[m₁.m₂]）/ F
  即：r = √（6.67×10^-11牛米²/公斤².1 公斤 x 1 公斤）/ 1 N
  結果是 r = 8.16 x 10^-6米。