什麼是複利?概念、計算方法 、複利與簡單利息、 範例
概念定義
複利是指根據變動資本金額所產生的價值,並用於投資或貸款。
之所以稱為複利,是因為它是根據持續增加的資本價值計算,因為每個期間的利息都會相加。這個概念可用於計算你在投資或儲蓄中賺取多少,也可用於計算你在貸款或信貸上所支付的金額。
其主要特點是計算出的利息會以指數級變化,並會加到每個期間的本金價值(資本化)。因此,每個期間的利息都會較高。

以下你可以看到這些概念的範例,展示了資本800美元、複利率2%,在五個期間內的行為:
| 1 | 800美元 | 2% | $16.00 |
| 2 | 816.00 墨西哥索元 | 2% | 16.32美元 |
| 3 | MX$832.32 | 2% | 16.65美元 |
| 4 | $848.97 | 2% | $16.98 |
| 5 | $865.95 | 2% | 17.32美元 |
在上圖中,我們可以看到本金和利息的價值會隨著利息的資本化而逐漸增加,且每個時期都會有所變化。
計算方法
計算複利的一般公式如下:
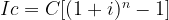
廣告內容,續見下文
上述公式中涉及的變數有:
資本(C):作為貸款或投資交付價值的初始金額。
該期間的利率(i),以小數形式表示。
時間(n):多個時期。
要應用上述公式,必須考慮利率與期間數必須在同一時間單位內表示。
若利率與期間數不在同一單位表示,則在套用公式前,必須計算適用於各複利期的利率,如下:
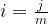
此公式涉及的變數包括:
比例利率(i):適用於每個複利期的利率。
利息(j):年利率。
時間(m):利息以一年為單位資本化的頻率。
複利與簡單利息
複利與簡單利息的主要差異如下:
在複利中,本金的價值會不斷變動且不斷增加,因為每個期間計算的利息會加到本金上。另一方面,單純利息是以初始資本價值計算,且初始資本保持不變。
複利中,利息產生更多利息,而單純利息則不會產生更多利息。
複利中,複利會在每個期間加到本金上,而在簡單利率中則不會加到本金上。
複利中,計算出的利率會隨時間增加。在簡單利率中,每個期間計算的利率始終相同,也就是說不會有變動。
舉例來說,讓我們看看兩個利益在相同資本價值下如何表現:
| 簡單利息 | |||
| 就這樣 | 資本價值 | 利率 | 簡單時期利息 |
| 1 | 800美元 | 2% | 16美元 |
| 2 | 800美元 | 2% | 16美元 |
| 3 | 800美元 | 2% | 16美元 |
| 4 | 800美元 | 2% | 16美元 |
| 5 | 800美元 | 2% | 16美元 |
| 複利 | |||
| 就這樣 | 資本價值 | 利率 | 複雜時期利息 |
| 1 | 800美元 | 2% | $16.00 |
| 2 | 816美元 | 2% | 16.32美元 |
| 3 | MX$832 | 2% | 16.65美元 |
| 4 | MX$848 | 2% | $16.98 |
| 5 | 865美元 | 2% | 17.32美元 |
範例
範例 #1
Scandina Enterprises 公司獲得了價值 7,800 美元的免費投資貸款,並需以每年 25% 的複利利率支付三年,複利頻率為每年一次。你必須支付多少利息?
查看解決方案
Ic = C [(1 + i) n – 1]
CI = 7.800 [(1 + 0.25) 3 – 1]
Is = $7,434.38
回答:三年複利的價值為7,434.38美元。
範例 #2
Scandina Enterprises 公司獲得了價值 7,800 美元的免費投資貸款,並需以每年 25% 的複利利率支付 36 個月,複利頻率為每月一次。你必須支付多少利息?
查看解決方案
首先,我們會換算每個月適用的利率:
I = J/M
i = 0.25/12
i = 0.02083
現在我們有時間和利率在同一單位,這裡以月份為單位,我們可以應用複利公式:
Ic= C [(1 + i) n – 1]
CI = 7.800 [(1 + 0.02083)36 – 1]
置信區間 = 8,585.84
回答:36個月內複利需支付的金額為8,585.84美元。












