什麼是算術平均?概念、用途、計算方法、範例
概念定義
算術平均值,也稱為平均值,是將所有資料加總後除以總資料量所得到的數值。
統計分析面臨的一個基本問題是尋找能代表一連串數值的值;也就是說,如果你的數量在空間或時間上變化,你就必須取得其主要水準。
這個主要等級或等級所提供的價值即為平均值。
當計算算術平均值時,變異會被忽略,只關注主要值,這在統計摘要中是一大優勢。
算術平均值的值取決於構成該系列的各項指標,且會受到與平均值極大偏差的影響。

用途
算術平均數的用途如下:
算術平均是最常用的平均值,因為它可以對任何類型的級數進行計算,且偏好遵循算術級數的數列。
它適用於那些因為有零項或負項,無法計算某些平均值的序列。這種情況在齊次級數或構成它們的項間差異很大時也同樣存在。
在比例變異的情況下,也會使用算術平均值。
計算方法
算術平均值的數值是將所有資料加總後,再除以這些資料總數所得。
算術平均分為簡單與加權平均:
簡單:將系列中不同項賦予同等重要性,或用技術術語表達為相同權重、相同權重。
加權:即每項數值都受到一個量化因子完全改變的指標;如前所述,這個量化因素稱為權重或加權。
算術平均的符號為 ,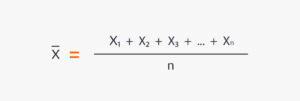
根據上述條件,計算 4、6、8、10、16、28 的算術平均值如下:
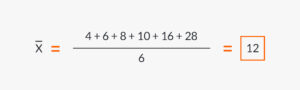
關於加權算術平均數,若你有一系列數值 X₁、X₂、X₃、...Xn,它們各自的權重為 P₁、P₂、P₃、...Pn,加權算術平均值由以下公式給出:
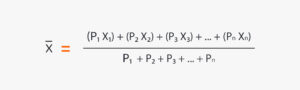
根據上述資料及以下數據,若某商品的不同單位以不同價格銷售,如下所示......
16個單位,8美元。
20單位,售價5美元。
18個單位,售價7美元。
…所售物品加權平均價格的計算方式為:

範例
簡單算術平均數
以下是參加1970年墨西哥世界盃的巴西國家足球隊22名球員的年齡:
| 球員生涯 | 年代 |
|---|---|
| 費利克斯 | 32 |
| 阿多 | 25 |
| 利奧 | 20 |
| 布里托 | 30 |
| 威爾森廣場 | 27 |
| 卡洛斯·阿爾貝托 | 25 |
| 馬可·安東尼奧 | 19 |
| 巴爾多奇 | 24 |
| 方塔納 | 29 |
| Everaldo | 25 |
| 喬爾·卡馬戈 | 23 |
| 瑪利亞 | 21 |
| 克洛多阿爾德 | 20 |
| 格森 | 29 |
| 敬酒 | 23 |
| 里韋利諾 | 24 |
| 保羅·塞薩爾 | 21 |
| 賈伊爾津霍 | 25 |
| 貝利 | 29 |
| 羅伯托 | 25 |
| 埃杜 | 20 |
| 達里奧 | 24 |
這些年齡總和為540年。為了確定冠軍隊每位成員的年齡,採用了墨西哥70世界盃舉辦時球員的年齡。
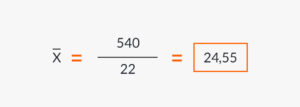
巴西隊平均年齡介於24至55歲,曾在1970年墨西哥世界盃上令足球迷驚艷,至今仍是史上最年輕的奪冠隊伍。
加權算術平均
在公司 Example, C.A. 中,100 名員工的薪資分布如下:
| 沒有。工人 | 月薪以美元計算 |
|---|---|
| 40 | 800 |
| 25 | 1.000 |
| 20 | 1.250 |
| 15 | 1.500 |
上述資訊的順序如下:
| X | 薪資 | 800 | 1.000 | 1.250 | 1.500 | |
| P | 權重 | 40 | 25 | 20 | 15 |
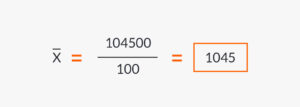
為了決定加權算術平均數,資訊會按以下方式完成:
| X | 800 | 1.000 | 1.250 | 1.500 | 總計 |
| P | 40 | 25 | 20 | 15 | |
| X*P | 32.000 | 25.000 | 25.000 | 22.500 | 104.500 |
根據此,加權算術平均的結果為: