物理學和數學中的向量是什麼？概念、含義、類型、特徵和示例

我們解釋了物理學和數學中的向量是什麼，它的含義、類型、特徵和示例。此外，向量的其他含義。

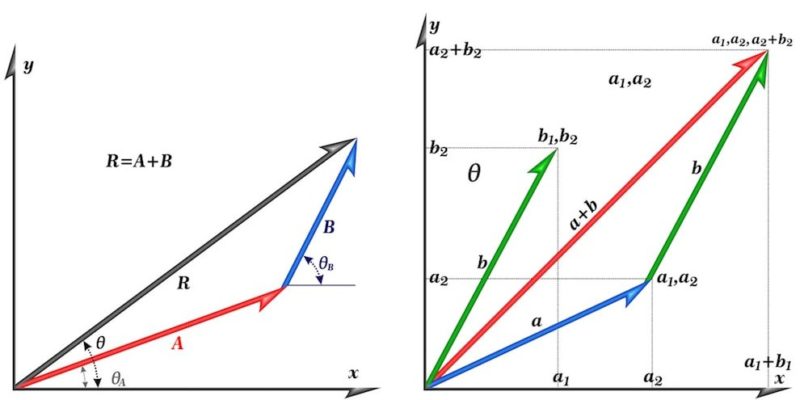
向量可以在笛卡爾平面中用 x，y 座標表示。

什麼是向量？

在物理和數學，向量是直線的一段，被賦予了含義，即在二維或三維歐幾里得平面內定向。換句話說，向量是向量空間中的元素。

向量允許我們表示物理量，這些物理量不僅具有強度，而且具有位址，就像強度、速度或位移.具有方向的這一特徵是向量大小與標量大小的區別。

此外，一個向量可以用笛卡爾平面使用一組座標 (x，y） 或三維 （x，y，z） 的 x，y，z。向量通常由所用符號上方繪製的箭頭表示。

• 另請參閱：物理學中的力學

向量的特徵

以圖形方式表示的向量具有以下特徵：

• 位址。定義為繪製向量的線，在空間.

• 模組或振幅。這經度在平面內等效於以數值表示的向量大小的圖形。

• 意義。由以圖形方式表示向量的箭頭表示，它表示向量前進的幾何位置。

• 應用點。對應於向量以圖形方式開始的位置或幾何點。

• 名稱或名稱。由圖形表示的向量附帶的字母表示，該字母與它表示的量級或其值的起點和終點之和一致。

向量的意義

向量的方向由指向某個方向的箭頭以圖形方式表示。這表示向量指向作用線（方向）的哪一側，即它指向的位置。

Sense 在表示向量大小時非常重要，因為它可以確定可以使用它們執行的作或計算的類型。

向量的類型

根據其應用點的位置，向量分為：

• Free 向量。那些沒有特定應用點的。

• 滑動向量。那些申請點可以是申請線中的任何一個。

• 固定或綁定向量。那些具有單一且確定的申請點的帳戶。

但是，也可以根據其他元素對向量進行分類，如下所示：

• 角度向量或併發向量。那些形成角度關於他們的行動路線或方向。

• 相反的向量。那些具有相同星等但方向相反的磁流。

• 共線向量。那些有著共同行動路線的人。

• 並行向量。那些行動路線恰好是平行的。

• 共面向量。那些作用線位於同一平面上的使用者。

向量示例

向量允許我們表示運動中涉及的不同力。

物理學使用笛卡爾平面中的向量來表示力的組合。

向量可以通過指向方向來表示相反的力。

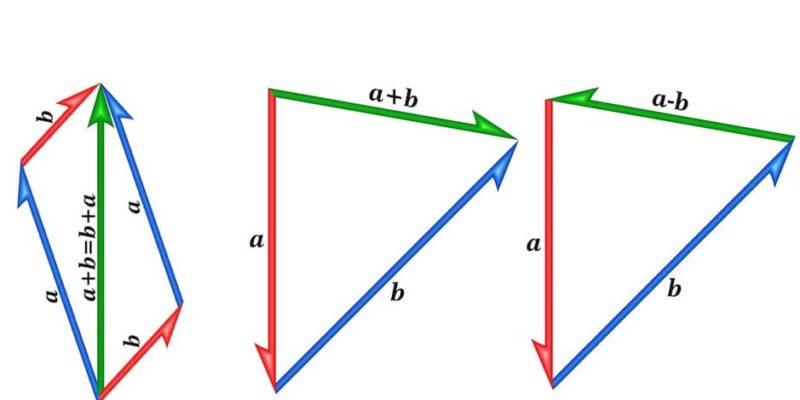
向量可以相互相加和相減。

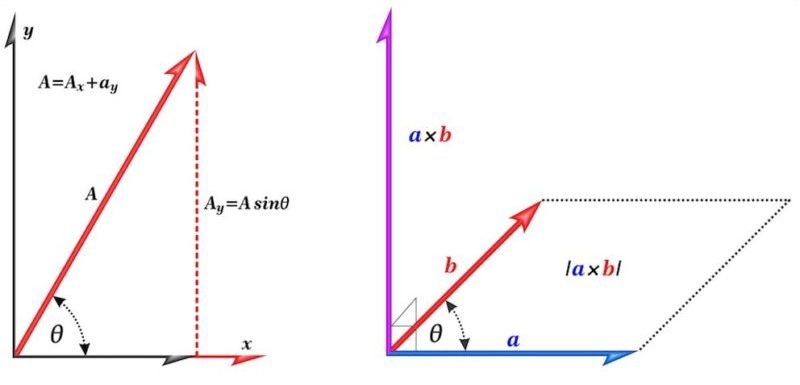                           在笛卡爾平面中，向量允許進行許多其他計算。

“向量”的其他含義

術語 向量也用於生物學，具有某種疾病或傳染源的“傳播機制”的含義。

例如，蚊子可能是許多疾病的媒介，這些疾病必然需要這種昆蟲的叮咬才能傳播到人.這些媒介不由自主地為傳染源的成熟和地理或人群傳播服務。

另一方面，我們也在空間導航領域中談到向量，如同義詞“航天飛機”的“航天飛機”，即允許其他小型飛行器到達外太空的太空運載火箭。