什麼是描述性統計?概念、指標、範例
概念定義
描述性統計是一種統計,試圖濃縮或總結一連串數值的所有資料或特徵,以描述序列中的某些面向,也被稱為演繹統計。
此方法是一種相對簡單且高效的資料摘要與特徵化方式,提供適當的呈現方式來呈現所收集的資訊。
描述性統計提出建議,說明如何以表格、圖表、圖表或圖表,清晰且簡潔地總結研究數據。在進行描述性分析之前,必須明確研究目標,並識別不同變數的測量尺度。

在描述性統計中,當取得研究資料時,有必要將其濃縮並以一個或多個數值來總結,這些數值決定了研究現象的主要特徵。構成這類統計方法的指標,正是能達成此摘要的指標。
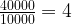
指標
描述性統計的主要指標如下:
-
比率、率與百分比:這些是相對的指標,用以濃縮某特徵在一組單位中的出現率資訊。
-
頻率分布:資料分組形式,將資料分成類別,每個類別展現其相應的頻率。
-
位置或中心傾向的度量:分為數學平均數:算術平均、幾何平均與調和分析;以及非數學平均值:中位數與模式。
-
離散度量:對於量化變數,可識別的離散度量包括平均偏差、標準差或標準差、四分位數範圍,以及最小值與最大值。
範例
比率、利率與百分比
原因
比值定義為表示兩個量之間量化關係的值。例如,若某地理區域有4萬名兒童在校,1萬名學生未上學,則已上學與未上學的比例可表示為商:
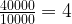
根據結果,可以說每四個在學校的孩子中,就有一個孩子沒上學。
速率
在比例或比率中,與前一個指數不同,商的分母是所列單位總數。以上述例子為例,學生在校與在校的比例為:
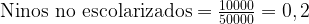
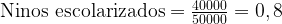
值得注意的是,當將兩個所得比率(0.80 + 0.20)相加時,結果為一(1),因為它們是互補比例。
百分比
如同率的例子所示,解以十進位數值表示,雖然從統計角度來看不成問題,但結果通常以百分比表示。這就是為什麼習慣將比例乘以100,將小數值轉換為百分比。
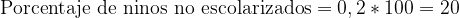
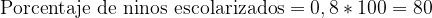
頻率分布
頻率分布是將資料分組到互斥的類別中,這些類別顯示每個類別中觀測值的數量,這為收集資料的分組增添了額外價值。
舉例來說,以下是一所中學學生運動偏好的頻率圖,該校有1,000名學生就讀。
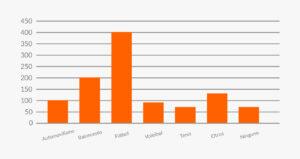
位置或中心傾向的衡量
舉例來說,以下是中心趨勢中最常用的三種指標:算術平均、中位數和小模式。
算術平均
這是透過將你所有資料的價值相加來決定的。結果再除以該資料總數。
算術平均數的計算方式如下:
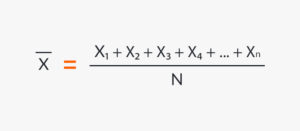
根據上述公式,以下一系列圖形的算術平均數可計算如下:
-
數字:5、9、10、12、16、19、22、27。
-
N = 8(資料數量)。
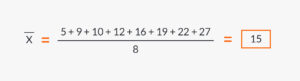
中等
此位置度量定義為將分布除以使兩邊各有相同數量項的值。
根據此定義,要確定中位數,必須對資料進行排序,而中位數的值可能與序列的某個值重合,取決於資料數量是奇數還是偶數。第一種情況是重疊的,第二種則不重疊。
如果你有一連串數值 X1 + X2 + X3 + ....... + Xn,依序從低到高排列,當項數數(N)為奇數時,中位數為 (N + 1) ÷ 2。當 N 為偶數時,公式為 (N ÷ 2) + 1。
舉例:
-
當值為 4 + 8 + 12 + 14 + 18 時,中位數會位於 12,因為它是奇數。5 + 1 = 6 ÷ 2 = 3(第 3 位)。若序列的測度數為奇數,則中位數即為該系列的中心分數。
-
值為:7 + 8 + 14 + 15 + 18 + 20,此例中項數為偶數,任何不小於14且不大於15的數皆可視為中位數,因為不超過N ÷2 = 3個觀測值少於中位數,也不會大於它。在這些情況下,通常會以14.5作為中位數,也就是14和15之間的中點。14 + 15 = 29 ÷ 2 = 14.5
時尚
它被定義為重複次數最多、最典型的系列值。在頻率分布中,它是項最密集集中的值。
一些常見的時尚例子包括:最常見的身高、最常見的薪資、最多重複的評分等等。換句話說,時尚是集中力達到最高點。
舉例來說,組成一支職業籃球隊的12名球員身高如下所示。
| 球員生涯 | 高度 | 球員生涯 | 高度 | 球員生涯 | 高度 |
|---|---|---|---|---|---|
| 1 | 1.79公尺。 | 5 | 1.95公尺。 | 9 | 2.04公尺。 |
| 2 | 1.87公尺。 | 6 | 1.95公尺。 | 10 | 2.04公尺。 |
| 3 | 1.89公尺。 | 7 | 1.95公尺。 | 11 | 2.10公尺。 |
| 4 | 1.90公尺。 | 8 | 1.99公尺。 | 12 | 2.15公尺。 |
這支籃球隊薪資中最常見的身高是1.95公尺。(3次)。
擴散度量
色散被理解為級數的數值彼此不同;色散會根據這些差異的大小大小而變大或更小。
範例:計算平均值偏離算術平均值。
在此過程中,絕對值的差異是相對於算術平均值計算的,步驟如下:
-
計算級數中數值的算術平均值。
-
計算級數值相對於其算術平均值的偏差。將這些偏差相加得到 Σ |x – x̄|。
-
平均偏差由以下公式計算:
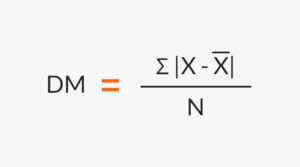
以下數列:4、8、12、16、20,其算術平均值為12,計算平均偏差的計算方法如下:
| X | |x – x̄| |
|---|---|
| 4 | 8 |
| 8 | 4 |
| 12 | 0 |
| 16 | 4 |
| 20 | 8 |
| 總計 | 24 |
結果是得到以下結果: