什麼是黃金比例?概念、特徵、歷史和例子
我們解釋了什麼是黃金比例,其歷史和黃金數量。此外,大自然和藝術中的黃金比例。

黃金比例出現在偉大的傑作中。[Botticelli,S。(c。1485)。金星的誕生] 。
黃金比例是多少?
它被稱為黃金比例,神聖的比例,黃金部分,黃金原因或黃金數字,以及其他名稱,是在自然界中發現並應用於藝術品的數學元素。從歷史上看,這個數字歸因於在感官上生成美學完美或宜人的構圖的能力。
黃金數是一個非理性的代數數(也就是說,它不能表示為簡單的部分,其值是無限的)。它用希臘字母phi(ϕ)表示,以紀念希臘雕塑家菲迪亞斯(500-431a。C.),儘管有時也有tau(τ),甚至帶有微小的alpha(α)。它的值等於1,618033988749894…,可以通過以下數學計算來表示:
ϕ =(1 +√5) / 2
儘管它以代數表示,但該數字是通過幾何形狀在古代發現的。根據代數方程,這是兩個(長度)和B (短)線的兩個段之間存在的關係或比例:
(a + b) / a = a / b
也就是說,總長度(a + b)與最長段(a)之間的關係等於最長段(a)與最短(b)之間的關係。這種關係稱為黃金比例。
這個數字的數學特性使藝術家和科學家著迷,因此在整個歷史上,它甚至被賦予了一些神秘的價值。自從發現以來,這一比例就以從樹木的葉子到烏龜的貝殼的自然圖案發現,並已被納入了偉大的傑作,例如文藝復興時期的繪畫或雅典巨大的巨大衛星。
另請參閱:美學
黃金比例的歷史
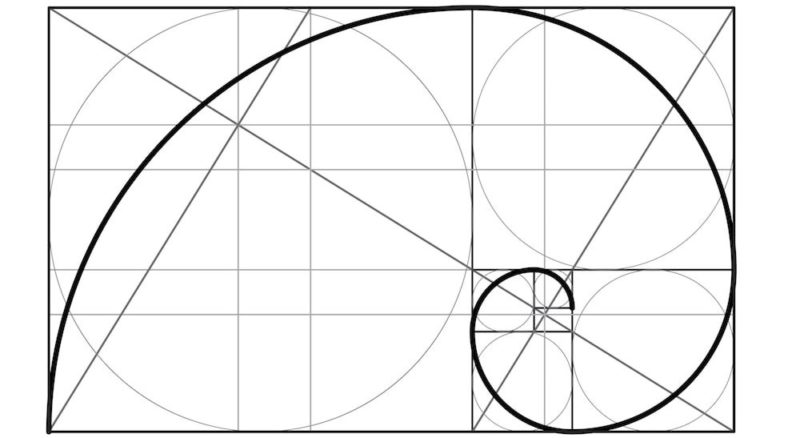
“ Durrero螺旋”基於黃金比例的重複。
根據考古發現的一些解釋,在2000年的美索不達米亞文化中。 C.使用了黃金比例,但沒有事先向古希臘的文檔有意識地證明其應用。
關於黃金數量的首次正式研究屬於歐幾里得哲學家(約公元前300-265章),他在他的書元素中證明了這是一個不合理的數字。其他研究也歸因於柏拉圖(c。427-347a。C .),儘管已經討論過這個想法。
1509年,意大利神學家和數學家盧卡·帕西奧利(Luca Pacioli)(約1445- 1517年)提出了他條約中的黃金數量的神聖品質。在其中,他將黃金比例作為神聖的隱喻,將三條線段與神的三位一體以及他無與倫比的整體聯繫在一起。
在這個想法的影響下,文藝復興時期的德國藝術家Alberto Durero (1471-1528)於1525年設計的金色螺旋形,後來被稱為“ Durero Spiral”,在其中他描述瞭如何用規則繪製的螺旋並根據áreea比例擊敗螺旋。
約翰內斯·開普勒(Johannes Kepler)(1571-1630)和馬丁·歐姆(Martin Ohm)(1792-1872)的作品中也提到了黃金比例。後者歸因於1835年的“黃金部分”一詞的創建,儘管有證據表明該名稱當時已經使用。
從那時起,黃金數字以Tau的希臘歌詞為代表,直到1900年,數學家Mark Barr(1871-1950)為希臘雕塑家Fidias致敬。
大自然

在許多形式的自然中,可以找到黃金比例。
ÁREA部分發現本質上的一些例子包括:
花椰菜品種的結構稱為羅馬牛西蘭花。
一些海洋動物的殼內部的螺旋。
石英晶體的生長模式。
花瓣的處置,例如瑪格麗塔酒和向日葵。
幾棵樹的葉子的肋骨(例如蕨類植物)之間的關係。
颶風的螺旋結構。
菠蘿皮質中存在的螺旋量。
肚臍在人體的總身高以及手的長度與前臂長度之間的關係相對於腳部的距離。
眾多蜘蛛種的織物。
朝鮮薊葉的排列。
黃金比例在藝術中的比例

希臘人是第一個故意發現和使用黃金比例的人。
黃金比例存在於以下藝術品中:
塔柱與雅典合夥人的雅典(公元前438年)之間的比例。
Leonardo da Vinci(1452-1519)撰寫的Gioconda或Mona Lisa的要素(1503-1519)之間的關係。
超現實畫家薩爾瓦多·達利(SalvadorDalí(1904-1989))與數學家Matila Ghyka(1881-1965)合作進行了Athomic Leda Work (1949) 。
塞爾格伊·艾森斯坦(SerguéieieieIsenstein,1898- 1948年)的電影樓梯(1925)的樓梯(1925)的階段,計劃的持續時間及其過渡。
巴黎圣母院大教堂的立面元素(1163)。
桑德羅·波蒂切利(Sandro Botticelli)(1445-1510)的繪畫金星的誕生(約1485年)。